When we look up at night and view the stars, everything we see is shinning because of distant nuclear fusion.
Carl Sagan
By far the most common types of stars in the Universe are red dwarfs, which are about as 40% massive as our Sun.[1]
Red dwarfs and the Sun, including many other stars, share a similar “surprising” characteristic, which is that they shouldn’t be capable of doing nuclear fusion or thermonuclear fusion (nuclear fusion using high temperatures).
And since red dwarfs are the most common stars in the universe, we could say, speaking classically – generally, stars are incapable of nuclear fusion.
In the eyes of classical physics, that means they shouldn’t be able to fight their very own gravity and should have collapsed under it.
Stars can be classified according to their surface temperature range:
| Class | Temperature (in Kelvins) |
| O | 30,000+ |
| B | 10,000–30,000 |
| A | 7,500–10,000 |
| F | 6,000–7,500 |
| G | 5,200–6,000 |
| K | 3,700–5,200 |
| M | 2,400–3,700 |
The Sun belongs to the G class and red dwarfs come under K or M, so it’s plausible to say, even some stars above the G class are also classically incapable of thermonuclear fusion.
But the Sun thrives still, as well as billions of red dwarfs and other stars throughout the Universe, of course, you see those bright twinkling stars.
As far as humanity is concerned, you and I wouldn’t exist without the Sun, but we do and that is because of an undervalued hero “quantum tunneling” in the Sun and other stars.
The only power source of stars is thermonuclear fusion, which helps them fight their own oppressive gravity to prevent a gravitational collapse, and generally, stellar cores are “classically” incapable of nuclear fusion, very ironical.
This is because atoms fusing have to overcome the coulombic repulsion (or force) between their positive nuclei and to overcome this repulsion, stars need to have high enough core temperatures, unlike most stars.
However, stellar temperatures are still more than enough to wipe out life on a planet.
For our discussion, we will focus on the qualities of the Sun.
Nuclear Fusion In the Sun
Unlike commonly presented, or interpreted by individuals, nuclear fusion inside stars is ‘slightly’ less straightforward.
Inside stars, it’s not just like hydrogen atoms directly come together and fuse into helium, instead, it’s a chain of fusion reactions going on.
A star spends most of its time in the “main sequence” (the Sun is a main sequence star), where it produces most of the energy by fusing hydrogen into helium.
In the main sequence, there are two dominant fusion reaction cycles, that stars use for fusing hydrogen into helium.
As for the Sun, the “proton-proton chain” or p-p chain is the dominant cycle that is used for hydrogen fusion and some energy comes from the CNO cycle or carbon-nitrogen-oxygen cycle.
Proton-Proton Chain Fusion Reaction Cycle
In the proton-proton chain reaction, since it’s a ‘chain’ reaction, multiple reactions happen consequently and energy is released in each step.
About 99% of the Sun’s energy comes from the various p-p chain reactions[2].
In the first step of the p-p chain, two protons fuse to create a deuterium.
$ p+p \rightarrow \ce{^{2}_{1}D}+e^{+} + v_{e} + 1.442 MeV $
1.441 MeV is the energy released in this case or the “Q value”.
One of the protons undergoes weak interaction during the fusion and transmutes into a neutron, which is a beta plus decay (β+).
Beta decays ‘rarely’ happen (‘why does it happen rarely?’, is beyond the scope of this article), which is also why the first step of the p-p chain takes a lot of time to proceed.
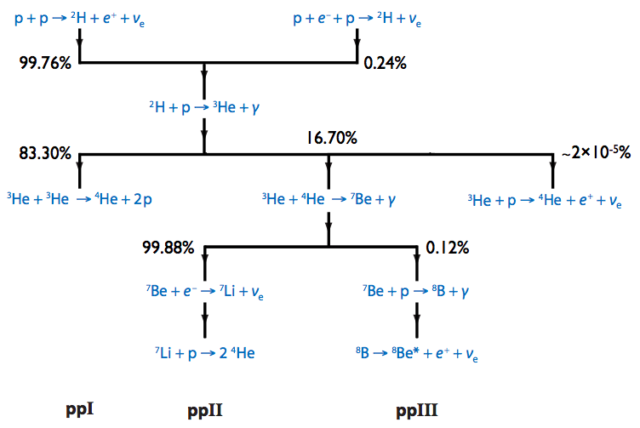
After this step, there are three branches or ways through which the reaction can proceed, but we will focus on the “p-p chain I” through which the reaction proceeds 83.3% of the time[3].
The p–p I branch
The Deuterium produced in the first step fuses with a proton and creates the Helium-3 nucleus.
The journey doesn’t stop here, there is more stuff that happens with the Helium-3 nucleus, but we will skip that for now.
$ \ce{^{2}_{1}D}+\ce{^{1}_{1}H} \rightarrow \ce{^{3}_{2}He}+\gamma + 5.493 MeV$
5.493 MeV is the Q value.
Coulomb Barrier or the Electric Potential Energy in Nuclear Fusion
When atoms come together to fuse, it’s like two proton balls coming together.
As you may figure, the protons would repel each other, this repulsive electric force between the nuclei fusing is known as the coulomb barrier (also a potential barrier or well).
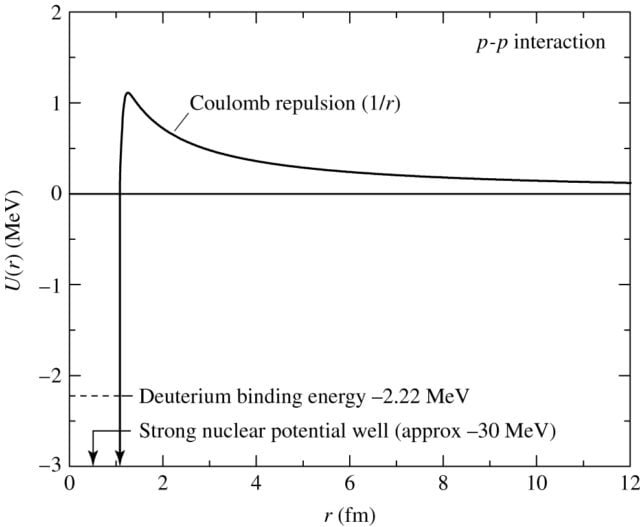
The energy required for two-point charges, like protons, to reach a separation ‘r’ can be given by:
$$U=\frac{e^2}{4\pi\epsilon_{0}r}$$
Where, $\frac{1}{4\pi\epsilon_{0}}$ = Coulomb’s Constant = 8.9875517923×109.
For a nuclear reaction to occur, the two nuclei must be within the strong force’s interaction range (~10-15 meters).
If the nuclei successfully overcome the coulomb barrier, the strong nuclear force dominates the electromagnetic force at that distance and holds the nuclei intact.
Relationship of Temperature and Nuclear Fusion
For atoms to surpass the coulomb barrier and fuse, they must have enough energy which is just their kinetic energy.
The temperature of any classical ideal gas system is proportional to the average kinetic energy of particles inside the system.
$KE_{avg}\propto T$
So, the higher temperature of stars will indicate higher kinetic energy of the ‘most’ of the atoms inside them.
Core Temperature Required for Nuclear Fusion (Classically) in Sun
The present core temperature of the Sun is about 1.5×107 K or 15,000,000 Kelvins.
We can evaluate the classical temperature required for nuclear fusion by calculating the energy required to fuse the nuclei, which is the height of the coulomb barrier between the nuclei:
$$V_c = \frac{e^2}{4\pi\epsilon_{0}}\frac{Z_{a}Z_{b}}{R_{a}+R_{b}}$$
Vc is the height of the Coulomb barrier, Za & Zb are the atomic numbers of the nuclei involved, and Ra & Rb are the radii of the nuclei involved which is in our case, we consider a deuterium and a proton.
Note that this is just the same equation as for the energy required for two point charges to reach a separation ‘r’ (see Coulomb Barrier in Nuclear Fusion), but we have two nuclei here instead of point charges.
However, while doing this we would be considering the nuclei coming close together as if they were touching each other, which is not required.
We just need to get them close enough to be inside the effective range of the strong nuclear force, which is about 1 femtometer or 10-15 meters, although this isn’t a strictly definitive value because strong force is very powerful as we approach 0.8 femtometers and decreases rapidly at distances beyond 2.5 femtometers.
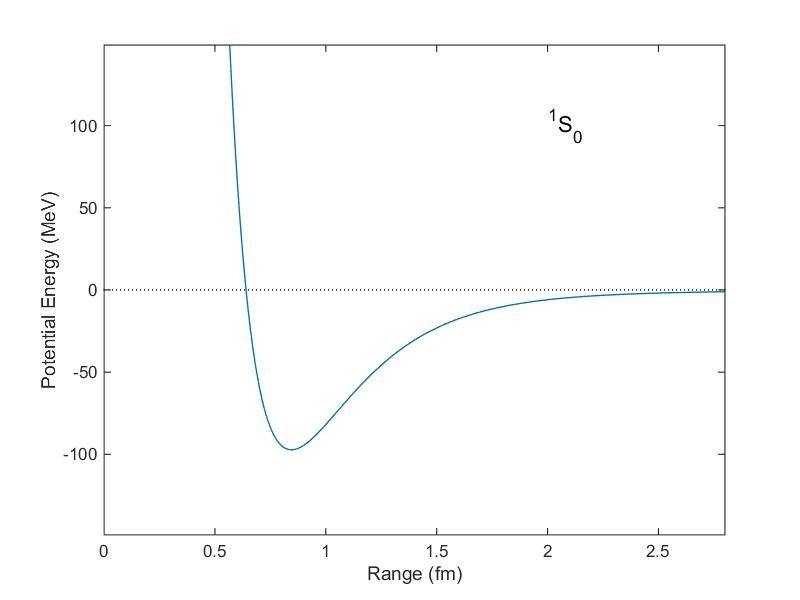
Now, if we use 10-15 meters instead of the sum of Ra and Rb in the equation it becomes:
$$V_c = \frac{e^2}{4\pi\epsilon_{0}}\times\frac{Z_{a}Z_{b}}{10^{-15}}$$
Since we have deuterium and an H+ nucleus (a single proton) both the atomic numbers Za and Zb are 1.
$$V_c = \frac{{(1.602 \times 10^{-19}})^{2}}{4\pi\epsilon_{0}}\times\frac{1\cdot 1}{10^{-15}}$$
That gives us 2.3071972 × 10-13 Joules, so the thermonuclear fusion of a deuterium with a proton or a hydrogen atom will need an energy of approximately 1.44 MeV (1 Joule = 6.242 × 1012 MeV), which is the kinetic energy required for the fusion.
Since the interior of a star contains a mixture of ions, electrons, and radiation (photons), for most stars (except very low-mass stars and stellar remnants) the ions and electrons can be treated as an ideal gas.[4]
So we can now consider the Sun’s core to behave like an ideal gas system, and then we can approximate the temperature required to provide this energy as average thermal energy for each particle using the following equation:
$$KE_{avg}=\frac{3}{2}kT$$
Here, KEavg is the average kinetic energy, k = 1.38066×10-23 Joules/Kelvin, is the Boltzmann Constant, and T is the Temperature required.
The equivalent temperature required for the given average kinetic energy of 2.3071972 × 10−13 Joules evaluated through that expression is approximately 1.114 × 1010 Kelvin or 11,140,000,000 Kelvin.
Considering a “head-on collision” between the fusing nuclei, we could cut the temperature’s value in half, which will be 5.57 × 109 K or 55,70,000,000 Kelvin.
The sun’s core temperature of 1.5 × 107 K is just about 0.27% of the required 5.57 × 109 K, while the exact values may differ, the difference of an order of 102 will be consistent.
How Quantum Tunneling Helps Nuclear Fusion in the Sun?
Multiple fusion reactions take place inside the Sun, and it’s mostly quantum tunneling in the Sun that makes it possible. The concept of “quantum tunneling” portrays a picture of a particle as a probabilistic wave.
For a quantum particle that is encountering a potential barrier from a side, there is a non-zero probability for that particle to exist on the opposite side of the barrier.
While “non-zero” is also to say that the probability is very small, quantum tunneling also depends upon the energy of the particle and the frequency of the collision of particles with the barrier.

In gigantic systems of blistering temperatures as that of stars, where there are zillions-zillions of atoms, the significance of the small tunneling probability of individual particles gets devalued to a certain extent.
So, stars just have to have enough energy so that the fusing nuclei can come close enough to quantum tunnel and fuse which might not necessarily be in the range of the strong nuclear force.
The lack of energy of the nuclei in this case is a classical physics problem, and a particle quantum tunneling through a potential is righteously counterintuitive.
In the classical world, If you roll a ball up a ramp, it’ll climb up the ramp if you roll it fast enough, but if you don’t, it’ll just come back rolling down and that’s simple, no other alternative events can take place.
How does a quantum particle then cross a coulomb barrier without enough energy?
In the quantum world, for a short time interval $\:\Delta t$) you cannot precisely measure the energy of a quantum particle, there will be an uncertainty $\:\Delta E\:$ in the measurement.[5]
This is a form of the Heisenberg Uncertainty Principle for simultaneous measurements of energy and time, given by the expression:
$$\Delta E \cdot\Delta t\geq \frac{h}{4\pi}$$
The equation implies that for a short time interval, a quantum particle can have an indefinite amount of energy, which is sometimes enough to surpass the potential well, weird but true.
Other Factors that Help Nuclear Fusion in the Sun
In our estimate of the temperature required for the Sun’s core to facilitate nuclear fusion, we initially calculated the average kinetic energy needed by the nuclei to undergo fusion.
It’s important to understand that this ‘average’ kinetic energy represents the most probable energy state for the particles within the Sun, but not the only one.
In reality, particles in any system, including the Sun, exhibit a range of energies and velocities.
This variability in particle energies is important for the process of nuclear fusion in stellar cores.
While many particles will indeed have the average energy, there are always some particles that have significantly higher or lower energies.
We use the Maxwell-Boltzmann Distribution, a fundamental concept in statistical mechanics, to study this phenomenon.
The Maxwell-Boltzmann Distribution shows that in a system at thermal equilibrium – like the Sun’s core – particle energies follow a specific pattern.
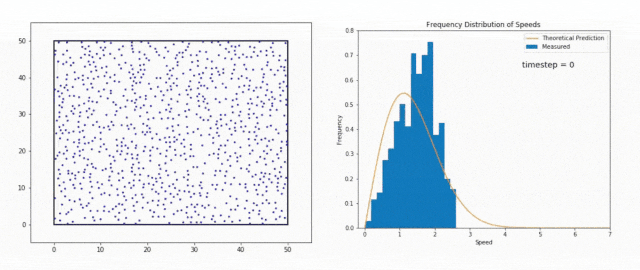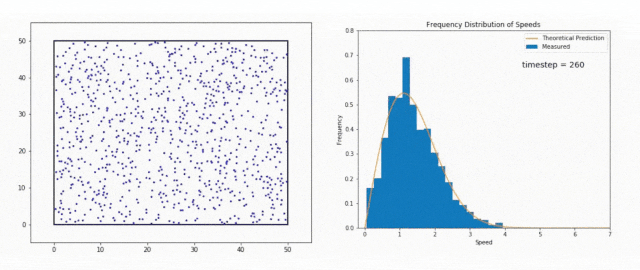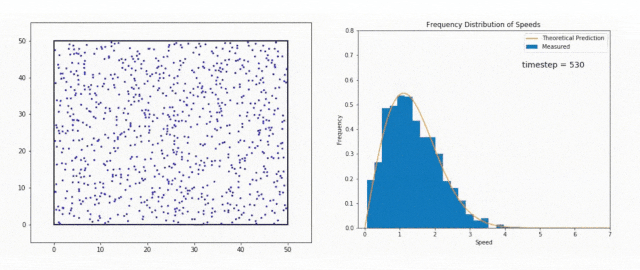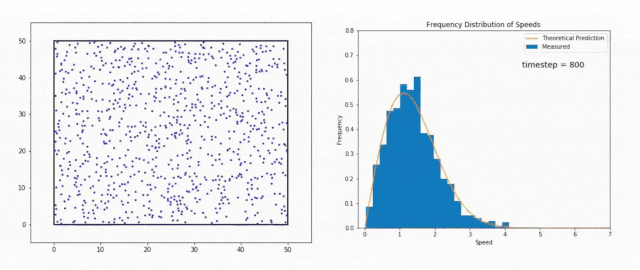
Most particles have energies around the average value, but there is a tail in the distribution that includes particles with much higher energies.
These high-energy particles are less common, but they are vital for stellar fusion, especially at temperatures where the average energy is not sufficient to overcome the Coulomb barrier, the natural electrostatic repulsion between positively charged atomic nuclei.
Interestingly, this distribution also sheds light on the role of quantum tunneling in nuclear fusion.
While the high-energy tail of the distribution accounts for some particles having enough energy to overcome the Coulomb barrier classically, a significant number of fusion events occur between particles with lower energies.
These particles can fuse thanks to quantum tunneling as we just discussed in the section above.
Likelihood of Fusion Reactions – Gamow-Sommerfeld Factor
The Sommerfeld Factor or Gamow factor or Gamow-Sommerfeld factor is used to understand nuclear fusion inside stars as it describes the probability of fusion reactions occurring at a given temperature and energy.
It was first introduced by the physicist Georges Gamow in the 1920s as a way to understand the rate of radioactive decay of certain isotopes.
As explained earlier, according to classical physics, it’s unlikely for protons to fuse due to the coulomb barrier, at temperatures commonly seen in fusion, such as those found in the sun.
However, when George Gamow applied quantum mechanics to the problem, he discovered that there was a significant probability for protons to fuse through the process of tunneling, this finding allowed for a better understanding of how fusion can occur at such low temperatures.
The Gamow factor is the probability of two nuclear particles overcoming the coulomb barrier, which is given by the following equation:
$P_{g}(E) = e^{-\sqrt{\frac{E_{g}}{E}}}$
E is the energy of the particle.
Eg is the Gamow Energy = $2m_{r}c^{2}(\pi\alpha Z_{a}Z_{b})^{2}$,
mr is the reduced mass of the two particles: $\frac{m_a m_b}{m_a+m_b}$,
α is the “fine structure constant“, c is the speed of light, Za and Zb are the respective atomic numbers of the nuclei involved in fusion.
The higher the energy (E) of the particle the, higher the probability of the nuclei overcoming the coulomb barrier.
In the world of the very small, where particle and wave aspects of reality are equally significant, things do not behave in any way that we can understand from our experience of the everyday world…all pictures are false, and there is no physical analogy we can make to understand what goes on inside atoms. Atoms behave like atoms, nothing else.
John Gribbin, In Search of Schrödinger’s Cat: Quantum Physics and Reality
Recommendations
Devesh Sharma, ‘How do Stars Work?’, Evincism, https://evincism.com/how-do-stars-work/
Dr. Don Lincoln, Why is the Weak Force weak?, Fermilab (YouTube), https://www.youtube.com/watch?v=yOiABZM7wTU
Pranav Mahapatra, ‘The Quantum Tunneling Effect – How does it work?‘, Evincism, https://evincism.com/how-does-quantum-tunneling-work/
Devesh Sharma, and Vikrant Singh, ‘Quantum Mechanics Explained: Mathematical Guide for Beginners‘, Evincism
References
- ‘Most common type of star’, Guinness World Records, “By far the most common class of star in our galaxy and the Universe are red dwarfs.”, https://www.guinnessworldrecords.com/world-records/87467-most-common-type-of-star[↩]
- ‘Solar fusion cross sections. II. The pp chain and CNO cycles,’ APS, p[7], “The relatively cool temperatures of the solar core favor the pp chain, which in the SSM produces ~99% of the Sun’s energy. The reactions contributing to the pp chain”, https://doi.org/10.1103/RevModPhys.83.195[↩]
- Case Western Reserve University, ‘Solar fusion cross sections II: the pp chain and CNO cycles’, 10 April 2010, p[8], https://arxiv.org/abs/1004.2318[↩]
- California Institute of Technology, ‘How Stars Work’, p[12], “Interior of a star contains a mixture of ions, electrons, and radiation (photons). For most stars (exception very low mass stars and stellar remnants) the ions and electrons can be treated as an ideal gas and quantum effects can be neglected.”, https://www.astro.caltech.edu/~george/ay20/Ay20-Lec7x.pdf[↩]
- Lumen Learning, ‘Probability: The Heisenberg Uncertainty Principle’, “This means that within a time interval Δt, it is not possible to measure energy precisely—there will be an uncertainty ΔE in the measurement.”, https://courses.lumenlearning.com/suny-physics/chapter/29-7-probability-the-heisenberg-uncertainty-principle/[↩]





