How do Rockets Work? – Rocket Science

A rocket is a cylindrical projectile that can be propelled to great heights or vertical distances by combustion of its fuel contents.

A rocket typically lifts off by expulsion of hot gases produced by burning fuel through the rocket’s engine, which exerts a force on the rocket and pushes it up.

Physics of Rockets

The physics of rockets is based on the principles of motion, particularly Newton’s Laws of Motion and Thermodynamics.

In terms of motion, a rocket works by generating a force, known as thrust, which propels the rocket in the opposite direction.

This is similar to how an object on the ground can be made to move by pushing or pulling on it.

And in terms of thermodynamics, a rocket propulsion system is required which consists of a rocket engine that works by burning fuel, which produces hot gases.

How does a Rocket Fly?

Rockets work on “Newton’s Third Law of Motion” which states that:

Every action has an equal and an opposite reaction

Newton’s third law of motion implies the Law of Conservation of Momentum, i.e. momentum is neither created nor destroyed, but only changed through the action of forces

Momentum ($\:p\:$) is the product of the mass ($\:m\:$) of a body and its velocity ($\:v\:$):

$p=mv$

And the conservation of momentum implies that the initial momentum of a system is equal to the final momentum of the system:

$p_{initial}=p_{final}$

Simply, to move forward, we have to leave something behind, so, to move up, rockets leave the stream of hot gases behind.

These gases are then expelled through a nozzle, generating a high-velocity exhaust stream that provides the necessary thrust to propel the rocket up.

The rocket moves with the same force as the exhaust gases moving out of the nozzle but in the opposite direction.

According to Newton’s Second Law of Motion, the rate of change in momentum implies the force acting upon the body. 

$f=ma$, where $\:a\:$ is acceleration.

Force is also equal to the rate of change in momentum ($\frac{dp}{dt}$) of the object to which the force was applied.

So whenever there is some force applied to an object, its momentum will change, which in other words is to say that the force accelerates the object.

The momentum ($p=mv$) of an object can change by changing either or both the mass or velocity of the object.

So, a rocket lifts up by the virtue of both losing mass (mass of the gases getting expelled) and also the thrust created by the (velocity) gases going out.

Putting things into perspective,

The gases coming out of the rocket have a certain momentum due to which they exert force on the rocket. As every force has an equal and opposite reaction, a force (in our case ‘thrust’) in the opposite-upward-direction is generated by the gas due to which the rocket lifts off.

The shape and design of the nozzle determine the direction and intensity of the exhaust gases, which in turn determines the direction and magnitude of the thrust.

The overall amount of thrust generated by the rocket depends on the amount of fuel burned and the velocity of the exhaust gases.

Expression for the Acceleration of a Rocket

Assuming you know some calculus, otherwise, things may get horrific for you here.

Consider a rocket lifting off.

Let, the mass of the rocket is $\:m\:$, the velocity of the rocket be $\:v\:$, and the velocity of the gases expelled out of the rocket $\:v_g\:$

Initially, the rocket is at rest, and so the momentum $\:mv\:$ of the rocket is zero.

The rocket starts burning fuel and gradually starts lifting off.

So we can say after some time $\:dt\:$, some small mass of gas $\:dm\:$ is expelled from the rocket, and the rocket gains some velocity $\:dv\:$.

The momentum of the rocket is now $\:(m-dm)(v+dv)\:$

As the gas is expelled out with the velocity $\:v_g\:$ and has some mass $\:dm\:$, it also has some momentum by the virtue of which it exerts a force on the rocket.

Note that although the rocket velocity $\:v\:$ is measured with respect to Earth, the exhaust gas velocity $\:v_g\:$ is measured with respect to the (moving) rocket.

So, measuring with respect to the Earth, the exhaust gas has velocity $\:(v\,+dv\,-\, v_g)$.

Now, the momentum of the exhaust gas will be:

$dm(v\,+dv-\,v_g)$.

So now, the momentum of the rocket becomes:

$(m+dm)(v+dv)+dm(v\,+dv-\,v_g)$

Recall, that the momentum is conservation:

$p_{initial}^{rocket}=p_{final}^{rocket}$

Therefore,

$mv = (m\,-\,dm)(v+dv)+d m(v\,+dv-\,v_g)$

Opening the brackets we get:

$mv = mv + md v\,-\,vdm\,-\,dmdv+vdm\,+dmdv-\,v_{g}dm$

Evaluating further we are left with:

$mdv= v_{g}dm$

Remember that the rocket is losing mass $\:dm\:$ so we should couple it with a negative sign:

$mdv= \,-\,v_{g}dm$

Now, by rearranging the equation we get to:

$dv = \,-\,v_g\frac{dm}{m}$

Dividing both sides by $\:dt\:$ we get:

$\frac{dv}{dt}=\,-\,\frac{v_g}{m}\frac{dm}{dt}$

Remember that due to the gravitational acceleration $\:g\,$=9.81m/s² of Earth reduces the momentum of the rocket going upwards, so factor it out, and $\:\frac{dv}{dt}\:$ is the acceleration of the rocket $\:a\:$.

So we have our final equation for the acceleration of a rocket:

$a=\,-\,\frac{v_g}{m}\frac{dm}{dt}\,-\,g$

Rocket Staging

Losing mass for a rocket is important to go up further.

If you have witnessed any rocket launch, you might have noticed that after reaching a certain height, the rocket breaks apart, and a smaller section of the rocket continues the journey leaving the other parts to free-fall.

So, the rocket does not only lose the mass of fuel, but it also keeps reducing its mass by dropping its part in the way – this is called rocket staging.

Staging is done to drop empty fuel tanks, which are now just useless mass for the rocket.

Dropping such mass would increase the rocket’s efficiency and reach the destination with the least fuel possible.

Nowadays, rockets consist of two or three stages.

Some even have strap-on boosters to provide initial thrust to the rocket, which detaches itself from the rocket once the fuel is consumed.

You’re required to learn the fundamentals of gravitation, escape velocity, and some vertical–angular motion dynamics to get the proper gist of what actually happens, however, we will not go into mathematics.

Rockets Need ‘Escape Velocity’ to Enter Space

Consider an object on Earth; whether it’s moving horizontally, vertically upwards, or at rest, the Earth’s gravity constantly acts upon the object.

So, when the object moves vertically upwards, it has to have a certain velocity to escape from the Earth’s gravitational influence; this velocity is called escape velocity.

Earth and all other planets, asteroid, and other massive bodies also have their own escape velocities.

The escape velocity of the Earth is 11.19 kilometers per second.

It can be determined by using a general expression from Newtonian mechanics:

$v_e=\frac{\sqrt{2GM}}{r}$

Here, $v_e$ denotes the escape velocity, $G$ is the gravitational constant, and $M$ is the mass of the body to be escaped from, in our case, Earth.

So the thrust generated by the propulsion system of a rocket must be enough to compensate for its mass and the earth’s gravitation and ensure that the rocket achieves the escape velocity.

Trajectory of a Rocket

The rocket fires up and lifts off, but where does it go?

It doesn’t go anywhere but revolves around the Earth or another planet or Sun in a certain orbit.

But how does a rocket achieve its position in outer space?

As the rocket generates thrust and moves through the air, it experiences aerodynamic forces, such as lift and drag, which affect its trajectory.

To control the flight of the rocket, it may be equipped with fins, flaps, or other control surfaces, which can be used to adjust the direction and orientation of the rocket in flight.

By carefully controlling the thrust and the aerodynamic forces, the rocket can be navigated to its desired destination

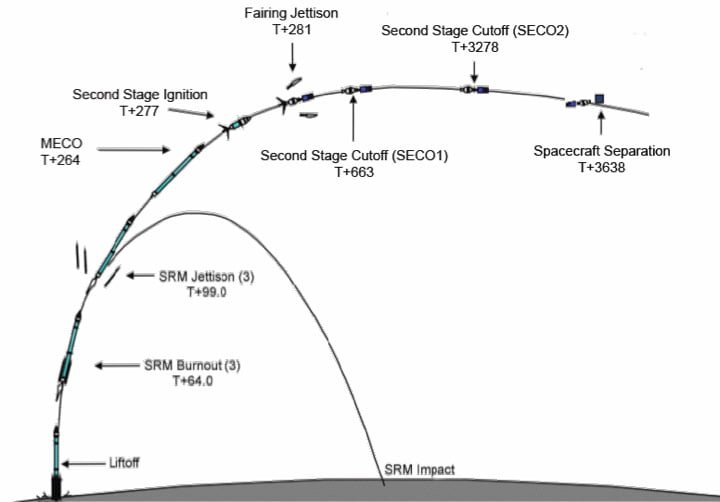
First, the rocket lifts off perpendicular to the ground and goes straight up.

Then it starts tilting slightly, and since now the rocket’s path is curved, it is performing a projectile motion.

It keeps burning fuel until the curved path becomes a circle or aligns with the Earth’s orbit, escaping the Earth’s effective gravitational influence.

An orbit is not a defined path – In physics, an orbit is a curved trajectory of an object like a rocket around a planet or any other massive body due to the body or planet’s gravity.

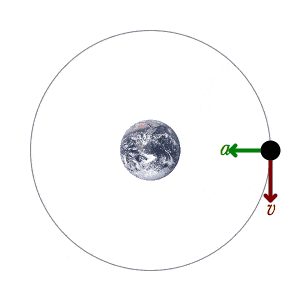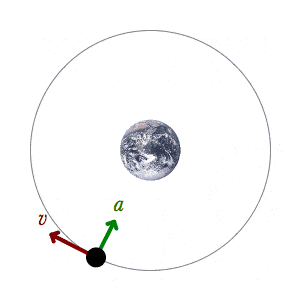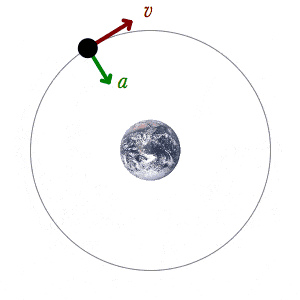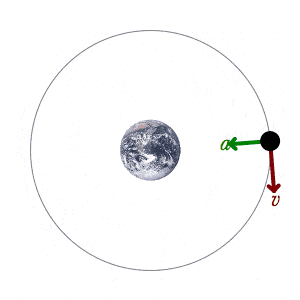
Orbital dynamics are a bit more complex than you may think.

After reaching the orbit, the rocket releases the payload or capsule which performs the designated task while moving along a certain orbit around Earth.

How do Rockets Work in the Vacuum of Space?

As explained, rockets work by using a combination of the principles of action and reaction, as well as Newton’s third law of motion.

In the case of a rocket, the action is the expulsion of gas from the back of the rocket, and the reaction is the forward movement of the rocket.

In the vacuum of space, where there is no air, a rocket still works by using the same principles.

The gas is expelled from the back of the rocket, and this causes the rocket to move forward.

The lack of air in space means that there is no atmospheric drag or resistance to slow the rocket down, so it can continue to accelerate as long as it has fuel to burn.

A commonly held misconception is that the rocket’s exhaust pushes against the ground to propel the rocket forward, but it doesn’t work this way.

Instead, the force that propels the rocket is the thrust generated by the exhaust gases.

In fact, the rocket’s thrust is greater in a vacuum than it is in the atmosphere or on the launch pad because it is easier to expel gases into a vacuum than it is to do so in the presence of air^[1].

One of the main challenges with chemical engine based rockets is that they must carry all of the fuel it needs to reach their destination.

This is because there is no air in space to provide the oxygen needed for the rocket’s engines to burn the fuel, so the rocket must carry its own supply of oxidizers in order to burn the fuel.

Rockets burn fuel using a combination of fuel and an oxidizer, which is a chemical substance that provides the oxygen needed for the fuel to burn.

The fuel and oxidizer are stored in separate tanks within the rocket and are combined and ignited in the engine.

This also leads to challenges in designing a rocket that can operate in the vacuum of space where the fuel and oxidizer must be stored in separate tanks, as they are clearly not compatible with each other.

So the fuel tanks must be carefully designed and constructed to prevent leaks and to ensure that the fuel and oxidizer are mixed and burned efficiently in the engine.

Recommendations

Pranav Mahapatra, ‘Rocket Propulsion Systems‘, Evincism

References

1. Introduction to Rocket Propulsion, Pressbooks, “It is a commonly held misconception that the rocket exhaust pushes on the ground(…)In fact, gases are easier to expel into a vacuum.”, https://pressbooks-dev.oer.hawaii.edu/collegephysics/chapter/8-7-introduction-to-rocket-propulsion/[↩]