The simple answer is–it’s because the Sun is the most massive object in the solar system.
Sun’s gravitational pull is massive as the Sun weighs around 1.989×1030 kg, to put this into your perspective, the Sun contributes about 99.8% of the entire mass of the solar system!
This is why it has the strongest gravitational field in the solar system, causing other planets to orbit around it.
But there’s more to the question as you try to dig further, if the Sun has such a strong gravity why do all the other planets including Earth and other objects not crash into the Sun? Or what is an orbit exactly?
Newton’s Laws of Motion and Gravity
Starting with the basics, in classical mechanics, we treat gravity as an attractive force between objects that have mass, and any object that has some mass possesses a gravitational field.
With the Universal Law of Gravitation Newton taught us that every massive object attracts any other object around it which is called Newton’s law of gravity, it looks like this:
$$F = – \frac{G m_1 m_2}{r^2}$$
Where $G$ is the Universal Gravitational Constant, $m_1$ is the mass of an object, $m_2$ is the mass of another object, and $r$ is the distance between the centers of the two objects.
You can now consider, $m_1 = M_{sun}$ or the Mass of the Sun, and $m_2$ to be equal to the mass of any other object in the solar system to find the gravitational force between them.
Due to the gravitational force between two objects, they cause each other to accelerate with respect to each other, however, the body with a greater mass has a larger influence on the other.
Let’s say we want to figure out the gravitational acceleration on a planet due to the Sun’s gravity we can start with the following:
$$F_{g} = M_{p}\cdot a$$
$$- \frac{G\cdot M_{s}\cdot M_{p}}{r^2} = M_{p}\cdot a$$
$$a = – \frac{GM_{s}}{r^2}$$
Here, $F_{g}$ is the force of gravity between the planet and the object, $M_s$ and $M_p$ are masses of the Sun and the planet respectively, $a$ is the acceleration on any planet due to the Sun’s gravity, and $r$ is the distance between them.
So we now know the force of gravity which is pulling everything towards the Sun, but what prevents the planet from falling into the Sun?
What Prevents Planets From Falling into the Sun?
Another force in action cancels out the effect of gravity which is caused by the nature of motion of those planets.
That force is called the centrifugal force, which is the reason why the string of a yoyo stretches when you swing it in the air.
Whenever an object performs a circular motion, it always experiences an outward force, it’s called a non-inertial force, which simply means it is experienced as a force whenever the frame of reference is rotating itself.
This is called the centrifugal force.
If you watch kids riding the merry-go-round, in your reference there is no outward force, but when you’re riding the merry-go-round yourself, which means you’re in the rotating frame, you would experience an outward force.
The outward force makes you feel like you’ll be thrown out of the merry-go-round ride.
Here comes Newton’s first law of motion–inertia to explain.
“An object at rest will remain at rest, and an object in motion will remain in motion with a constant velocity unless acted upon by a net external force.”
Because of inertia, the object in concern wants to travel in a straight path always, but since it changes its direction all the time in a circular motion, that gives the sensation of an outward force which is called the centrifugal force.
The kids riding on the merry-go-round, do not really experience an attractive force like gravity, pulling them toward the center of the merry-go-round structure.
It’s their seat connected to the center with a rod, that keeps them restricted in a place, and there is a tension force on that rod, directed towards the center, which is also called the centripetal force.
In planetary motion, we have the gravity of the Sun, which we treat as an attractive force that is pulling the planets toward the Sun, which is the centripetal force in this case.
Since the planets perform a circular motion around the Sun, they experience the same kind of outward centrifugal force that balances the gravitational pull of the Sun, which is why they orbit the Sun without falling into it.
However, again this centrifugal force isn’t a real force but is a result of the inertia and velocity of the object in a circular motion, the centripetal force is the real force.
Visualizing Orbits: Launching A Ball Into Space
A more fun way of imagining this orbit scenario is to suppose you throw a ball up away, what happens? it travels some distance in the air and falls.
Now throw the ball with more strength this time, what now? it went farther than before.
Try throwing it a few kilometers away, it might not be physically possible for you to do so, but let’s just assume you can.
Try with all you might and throw it 420 kilometers high. Did it fall?
If you did it right, you might find it greeting the Astronauts at the International Space Station, which is also orbiting the Earth 420 kilometers high.
If we assume you did it right, it would mean first that the ball reached an altitude of 420 kilometers, second, it had a curved trajectory, and third that it had enough velocity, which means it was at the orbital velocity required to have it orbit the Earth 420 kilometers high.
If you green-marked all the three requirements the ball will never come back and will keep falling under the Earth’s gravity, which means it would start orbiting the Earth.
It might sound a little counterintuitive, but think about it for a bit.
The orbital velocity for an object so that it orbits the Earth is given by:
$$V_0 = \sqrt{\frac{GM_{e}}{R}}$$
Here, $G$ again is the gravitational constant, $M_{e}$ is the mass of the Earth and $R$ is the distance between the center of Earth and the object, we can get the orbital velocity required to orbit the Sun by simply replacing it with a mass of the Sun, the distance.
And yes, an orbit is just the path followed by that object when it keeps falling to the central object but misses the surface because its path is curved.
Planets and all the other objects that revolve around the Sun have the required orbital velocities, which is to say while they are being pulled towards the Sun, they are also moving sideways fast enough that prevents them from falling into the Sun.
But how do planets get their velocities to start with?
Where Do Planets Get Their Initial Velocity From?
To answer that we have to delve into the “planetary formation”.
The most widely accepted theory for the formation of the Sun and planets is that it started when a giant molecular cloud of gas started collapsing under its gravity.
For any star system in the universe, the star is the first one to be born, which is also why it will–ideally, take up most of the mass–be the most massive in that system.
There is Interstellar medium (ISM) or just clouds of gas, distributed non-uniformly throughout the universe.
Whenever there happens to be a greater density of these clouds at a region in space, because of the gravity of that bunch of clouds at that region, it starts contracting and collecting more and more mass or gas from the surroundings.
As the cloud of gas contracts, it starts spinning because of the conservation of angular momentum.
Angular momentum describes the rotational motion of an object around an axis, it is the product of its rotational velocity and its size, which implies that as an object contracts, its rotational velocity must increase.
This collection soon becomes so large that the gathered clump’s gravity starts compressing its mass at a point, and eventually starts becoming hotter due to the collision between the contracting gas molecules.
This leads to the formation of stars, after the star is formed some remnant mass in the neighborhood here and there, leads to the formation of planets, and asteroids all with different rotational velocities.
Any object that did not have enough velocity crashed into the Sun already.
More on Gravity’s True Nature–It’s Not Really a Force
Up until now, the explanation of the orbits was based on classical laws of physics using Newton’s laws of motion and gravity.
According to Albert Einstein’s General Theory of Relativity, massive objects do not pull other objects around towards them, which is to say gravity is not really a force.
Massive objects distort the fabric of space-time in such a way that the object which was supposed to follow a straight line forever in a particular direction, seems to be taking a turn around that object.
What does that mean?
Einstein proposed that space and time are not independent but interconnected to each other and mass-energy density of a region defines the curvature of the space-time fabric.
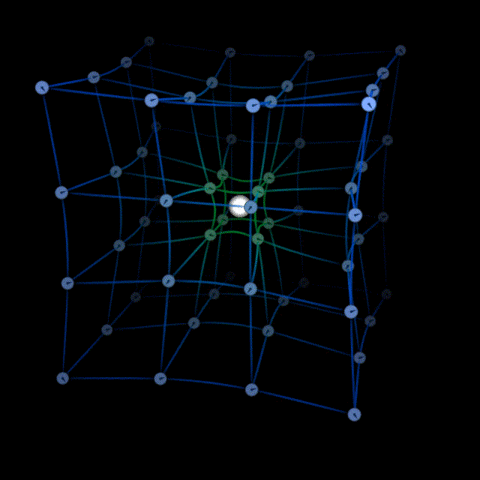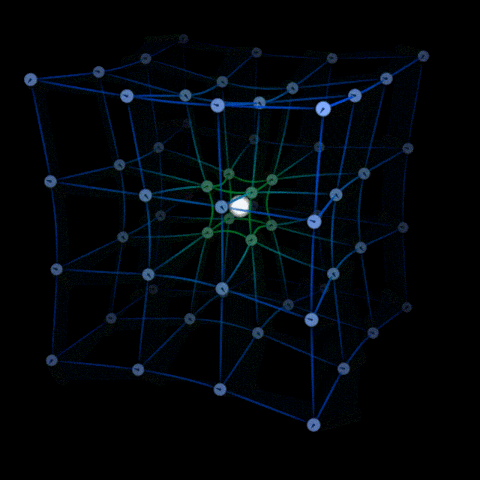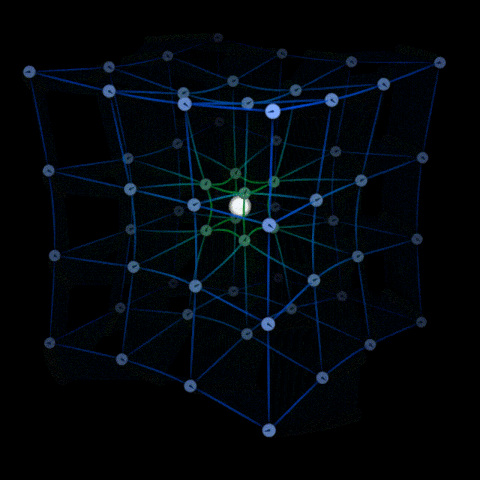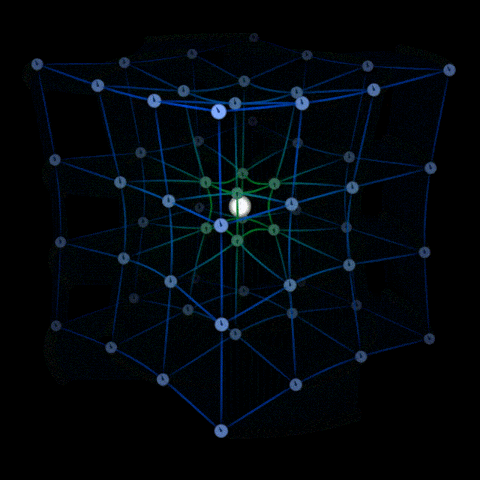
Due to the inertia of an object, it tends not to follow a straight line in our perspective but simply moves along the space-time curvature.
Imagine an ant walking on the paper, it’s walking a straight path over it.
Now bend that paper a little, for the ant, it’s still walking the straight path, but for you, it’s moving on a curved path.
Now, bend the paper in such a way that it’s joined end-to-end. What will happen?
The ant is now walking a circular path without needing to deviate from the straight line it’s been following.
That is how orbits work in General Relativity.
And peculiar enough, it turns out, any object wouldn’t follow a straight path in your perspective unless it is not under the influence of any other force, but it follows the shortest path given the curvature of space-time.
We call that path a geodesic, and these paths are the natural trajectories that objects would take in the absence of any other forces.
So you have a massive body curving the space-time around it (that’s gravity), for any other object in its vicinity, the path it takes while traveling from any point A to B will be the shortest and straight one for that object, although to you as an observer it won’t appear like a straight line.





